§2.3 反函数的导数，复合函数的求导法则

一、反函数的导数

设是直接函数，是它的反函数，假定在内单调、可导，而且，则反函数在间内也是单调、可导的，而且

(1)

证明： ，给以增量

由 在 上的单调性可知

于是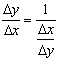

因直接函数在上单调、可导，故它是连续的，且反函数在上也是连续的，当时，必有

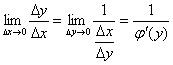
即：

【例1】试证明下列基本导数公式

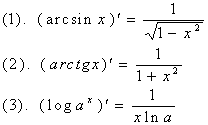
证1、设为直接函数，是它的反函数

函数 在 上单调、可导，且

因此， 在 上， 有

注意到， 当时，，

因此，

证2 设，

则，

在 上单调、可导且

故

证3

类似地，我们可以证明下列导数公式：

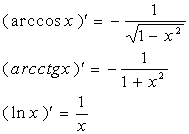
二、复合函数的求导法则

如果在点可导，而在点可导，则复合函数在点可导，且导数为

证明：因 ，由极限与无穷小的关系，有

用去除上式两边得：

由在的可导性有：

，

即

上述复合函数的求导法则可作更一般的叙述：

若在开区间可导，在开区间可导，且时，对应的 ，则复合函数在内可导，且

(2)

复合函数求导法则是一个非常重要的法则，特给出如下注记：

弄懂了锁链规则的实质之后，不难给出复合更多层函数的求导公式。

【例2】，求

引入中间变量， 设 ，，于是

变量关系是 ，由锁链规则有：

(2)、用锁链规则求导的关键

引入中间变量，将复合函数分解成基本初等函数。还应注意：求导完成后，应将引入的中间变量代换成原自变量。

【例3】求的导数。

解：设 ，则，，由锁链规则有：

【例4】 设 ，求。

由锁链规则有

(基本初等函数求导)

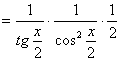( 消中间变量)

由上例，不难发现复合函数求导窍门

中间变量在求导过程中，只是起过渡作用，熟练之后，可不必引入，仅需“心中有链”。

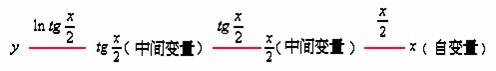
然后，对函数所有中间变量求导，直至求到自变量为止，最后诸导数相乘。

请看下面的演示过程：

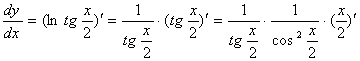
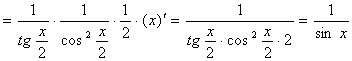
【例5】证明幂函数的导数公式 ，(为实数)。

证明：设